The Perceptron

Before neural networks, we had a perceptron -> a single neuron that makes a binary decision.

$$f(x)=\begin{cases} 1 & \text{if $w^\intercal{}x+b > 0$}\\ 0 & \text{otherwise} \end{cases}$$

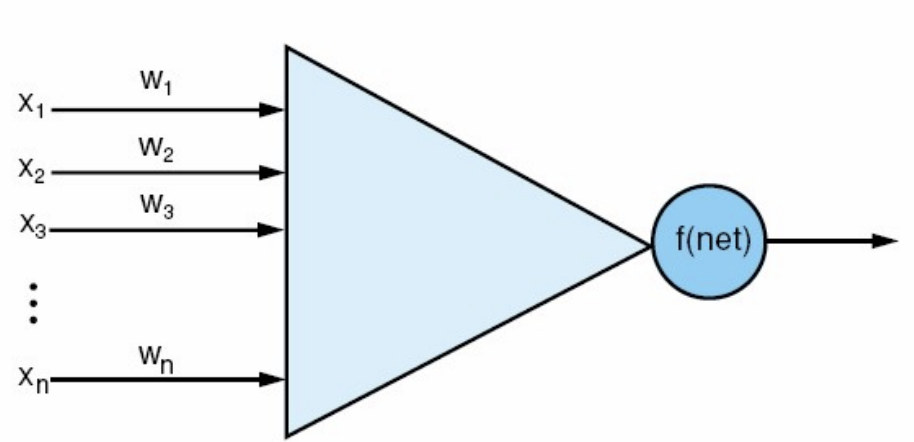
(linear algebra sidenote: dot product is $w^\intercal{}x$ because you can only do dot product of two matrices (m * n) and (p * q) if n = p)

A perceptron is a linear classifier. If we have a line that separates two classes:

• the weights $w$ decide the orientation of that line
• the bias $b$ decides where it sits (the offset)
• the perceptron output decides which side of the line the input lies on

It only works for linearly separable problems (where you can separate the two classes with a straight line) -> AND, OR, but not a XOR They can’t handle complex data.

Neural Networks

Each neuron computes two things:

• a linear function of the inputs $z = w^\intercal{}x+b$
• a non-linear function of that result $a = \sigma(z)$ -> activation function

So, each layer has two steps:

1. linear operator: multiply by weights -> $z = Wx$
2. pointwise nonlinearity: apply activation function to each element -> $a = \sigma(z)$ So a NN is just a repeated composition of these two steps: $f(x) = W_3\sigma(W_2\sigma(W_1x))$

We need an activation function that’s:

• non-linear: allows the model to learn complex, curved relationships, not straight lines
• differentiable functions: smooth enough that we can compute the gradients for training - so that backpropagation works

recall perceptron’s function: $y = \text{step}(w^\intercal{}x+b)$

• non-linear (because it jumps from 0 -> 1),
• BUT it’s not differentiable (cant compute gradient at the jump)

example of non-linear + differentiable functions:

• Sigmoid: $\sigma(x) = \frac{1}{1+e^{-x}}$
• tanh: $\text{tanh}(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}}$
• ReLU: $\text{ReLU}(x) = max(0, x)$

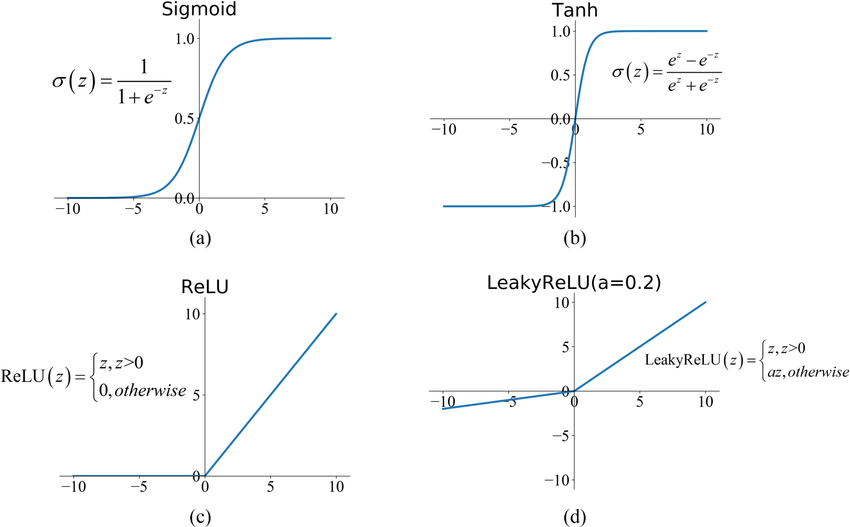
Image Classification

An image is a vector of numbers (pixels) $x \in \mathbb{R}^{32\times32\times3}=\mathbb{R}^{3072}$

…linear classifier?

$f(x, W) = Wx+b$This produces one score per class (cat score, car score, frog score, …), highest score wins. The problem is that each score is just a liner combination of pixel intensities. You can’t draw a flat decision boundary in pixel space! What if the cat moves slightly, or the lighting changes?

better, a multinomial logistic regression (we need probabilities)

Let’s use a Softmax function instead! $P(Y = k|X=x)= \frac{e^{s_k}}{\sum_j{e^{s_j}}}$ where $s=f(x, W) = Wx+b$

This converts raw class scores into probabilities that sum to 1 Then, we compute loss: $L = -\text{log}\:P(Y=y_i|X=x_i)$, penalizing the model if the correct class has low probability.

Feature extraction

Linear classifiers need data that’s linearly separable. Can we fix this by transforming the data into a new space where it becomes linearly separable? With feature transformations (color histograms, HOGs, bag-of-visual-words, etc…) Works okay, but:

• have to hand-design the transformations
• task-specific (what works for cars might fails for dogs)
• can’t adapt (if dataset changes, have to redesign features manually)

$x \rightarrow \phi(x) \rightarrow y$

• $x$: the raw input (e.g. pixels, audio wave, text tokens)
• $\phi(x)$: the learned representation (a non-linear transformation)
• $y$: the prediction or output (class label, next word, etc…)

In DL, $\phi(x)$ itself is learned automatically. Then the final layer can do a simple linear classification $y = \phi(x)^\intercal{}w$.

Neural networks learn the feature extraction for you (representation learning)

Each hidden layer performs a learned feature transformation. The final layer is still a linear classifier, but it now operates on learned features rather than raw pixels. And since the whole system is trained end-to-end (via backpropagation): the network learns whatever features make the final classification easiest.

We cannot teach a model how to pick up the thousands of subtle cues humans use to detect a cat, or a spoken word. Representation learning makes it so that models figure out those perceptual patterns automatically, even ones that humans didn’t even realize were there.

Reusability

The representations learned in one task often generalize to others. The first layers learn reusable “universal” features (edges, corners, colors, textures) The last layers specialize for our specific task (cat or dog?)

Supervised Representation Learning

Training with labeled data, the network learns both how to predict labels and how to represent inputs along the way.

Unsupervised Representation Learning

No labels, the model has to discover structure in the data itself (hopefully with a meaning). Auto-encoders (reconstruct input -> learn compressed representation)

When not to use DL?

• Smaller datasets can be easily solved with hand-crafted features and simpler classifiers.
• Good feature extractors exist (e.g. for tabular data), DL works best on perceptual data (images, speech, language)